Aug 30 2024 • 4 min read

OI #1: Chorus

Welcome to my first ever problem editorial! Here’s a link to the problem (the page links an English PDF as well).

Observations

First, it is worth noting that any valid arrangement must be an RBS, where A’s are replaced with ’(’ and B’s with ’)’ (convince yourself that this is true).

Therefore, we consider visualizing our arrangement as a walk on a 2D plane, where A’s are right steps and B’s are up steps (note that if our arrangement is an RBS, this graph should never cross the line $y = x$). Here’s the visualization for the arrangement “AABBABAABB”:

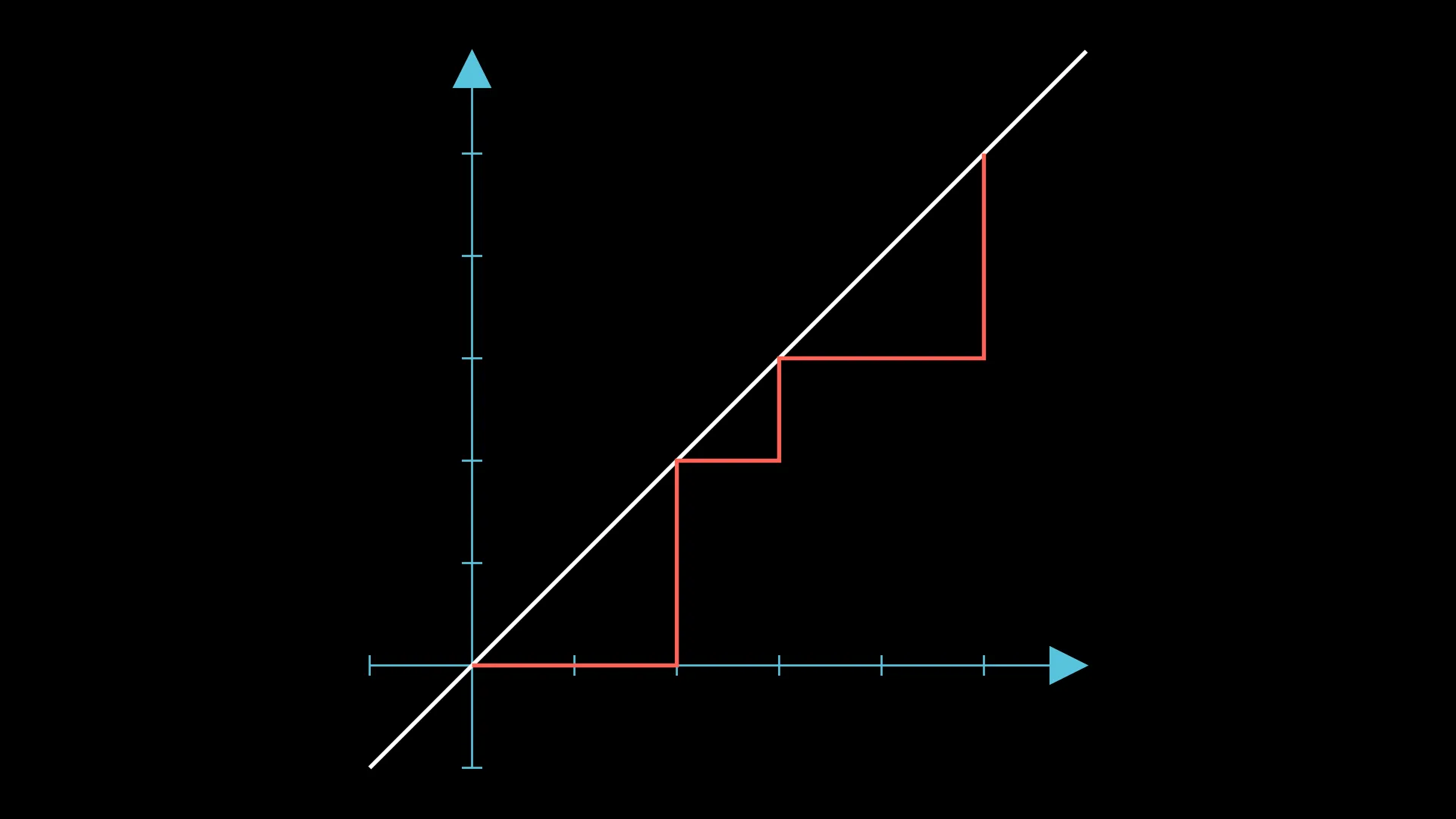
The maximum number of groups in this case is actually very obvious, since they are all contiguous—(AABB)(AB)(AABB). This can be seen visually as the number of times the walk touches the line $y = x$.

However, consider this case (which is one of the sample cases), “AABABABBAB”:

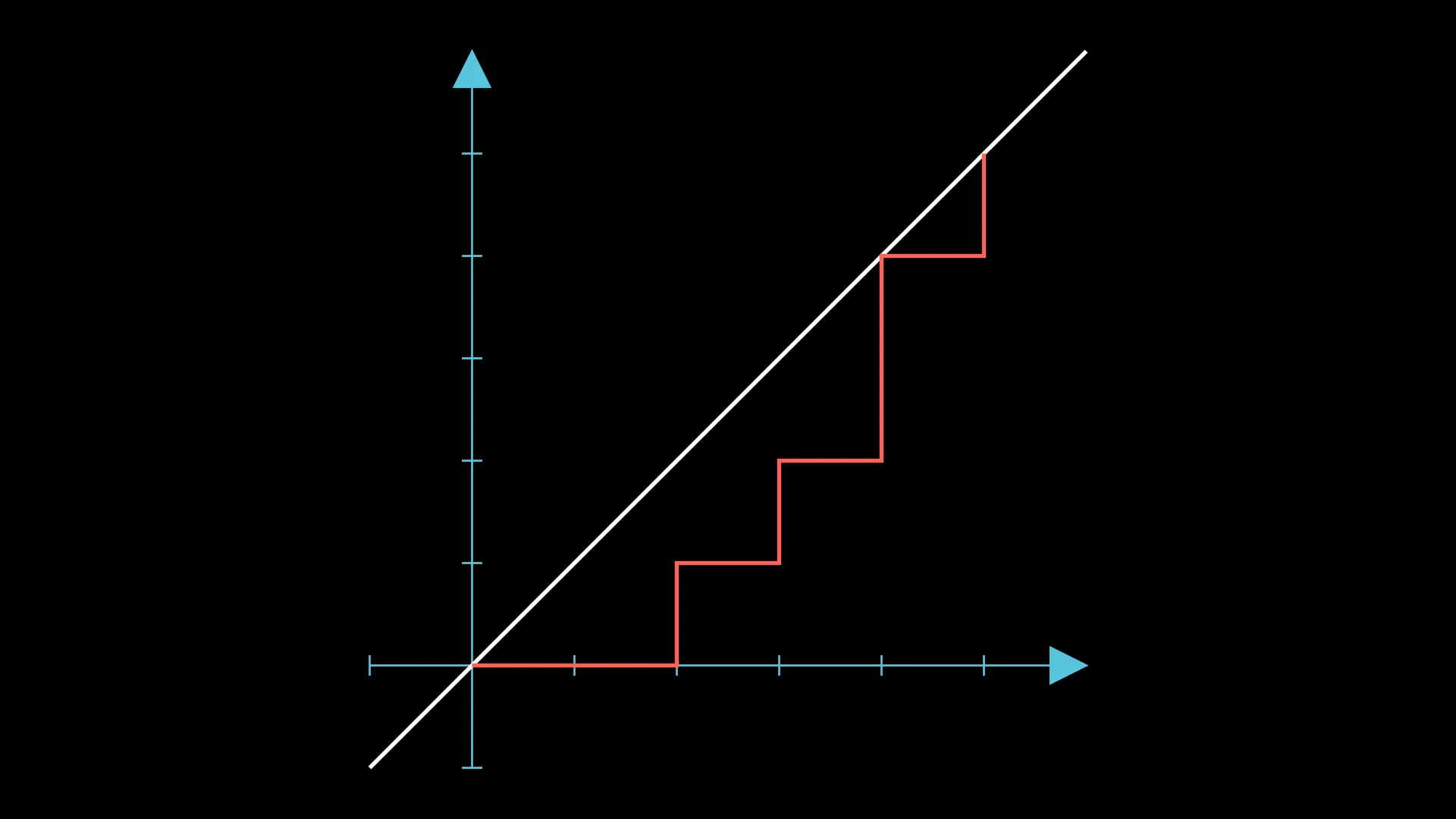
The maximum number of groups in this arrangement is also 3, but it is not as obvious as before. How can we transform this walk to make it easier to count the number of groups (i.e. such that the number of groups is exactly equal to the number of times the walk touches $y = x$)?

Here’s the same image, but with the groups colored this time:

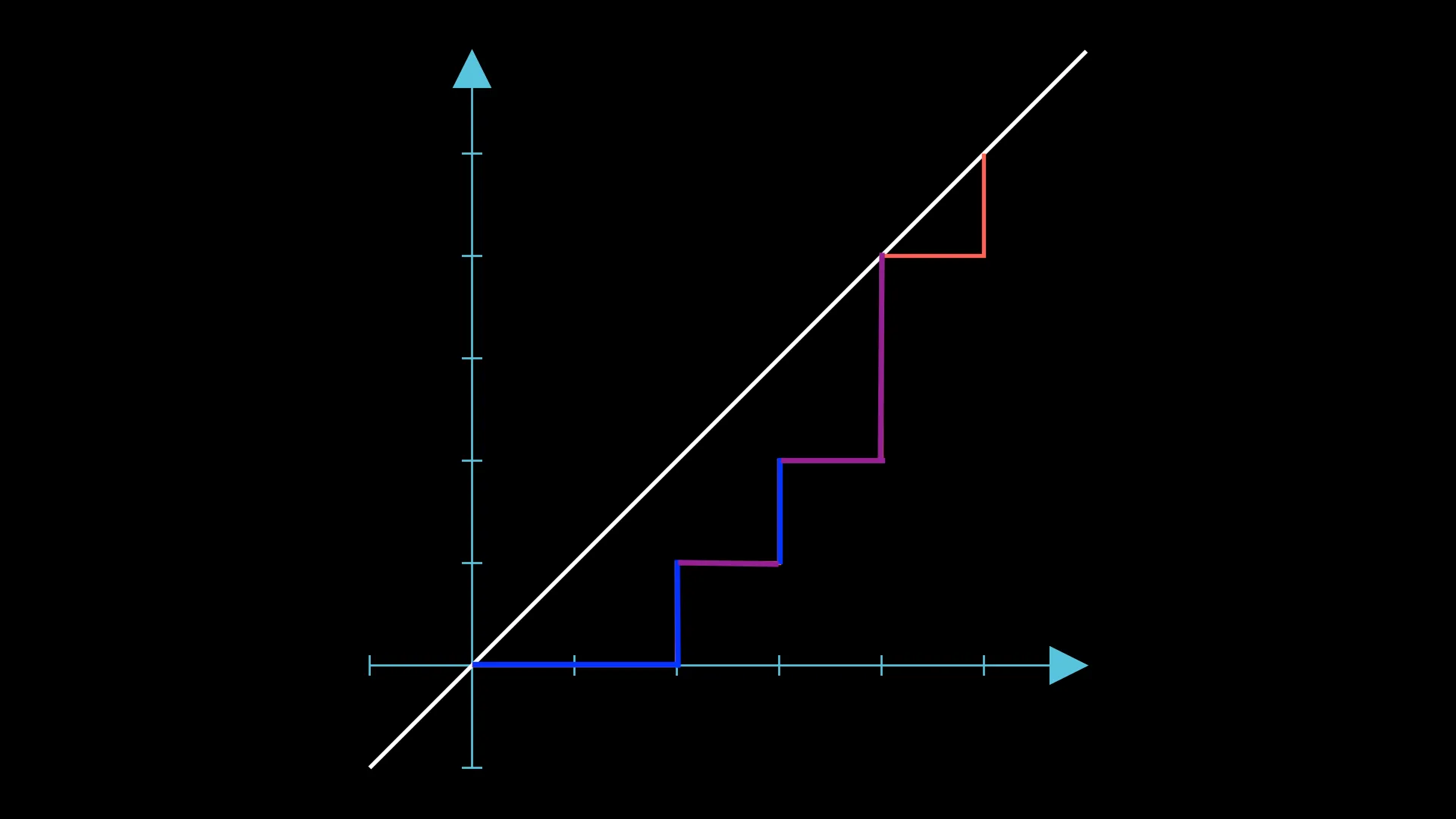
Notice how they are interleaved with each other; we would instead like every group to be disjoint. So, how can we achieve this?

Intuitively, we can “pull” the last blue segment forward and “push” the first purple segment up, which will give us this:

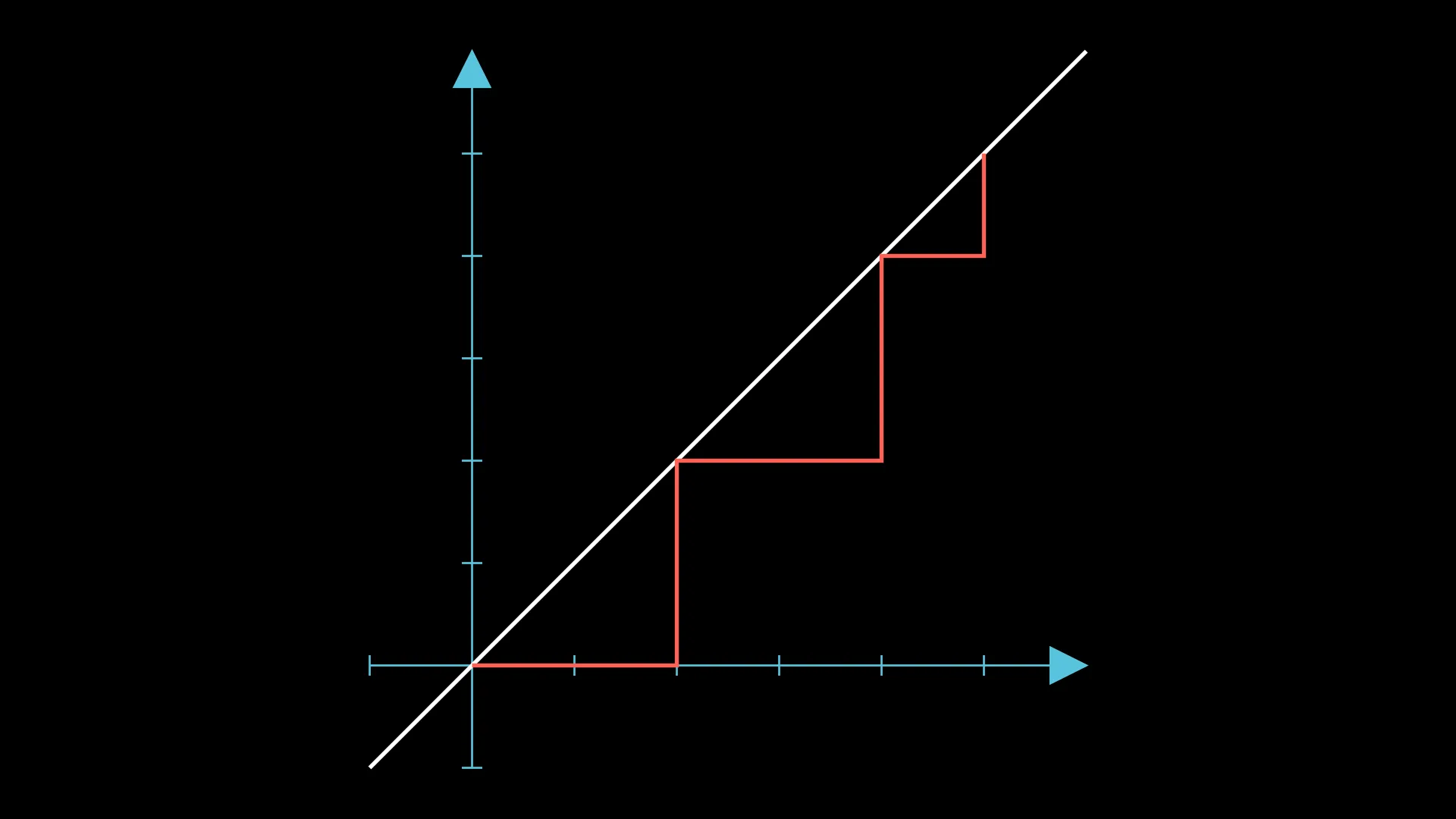
This can be seen even more intuitively as raising the height of a segment (in this case, the segment on $x = [2, 3)$).

Going back to the original problem, this operation is equivalent to swapping “AB” to “BA”, which can be shown to never actually decrease the answer (i.e. amount of groups formed).

So what operation will decrease the answer?

Consider the case where the initial arrangement is “ABABABABAB”. Here’s the walk for this arrangement:

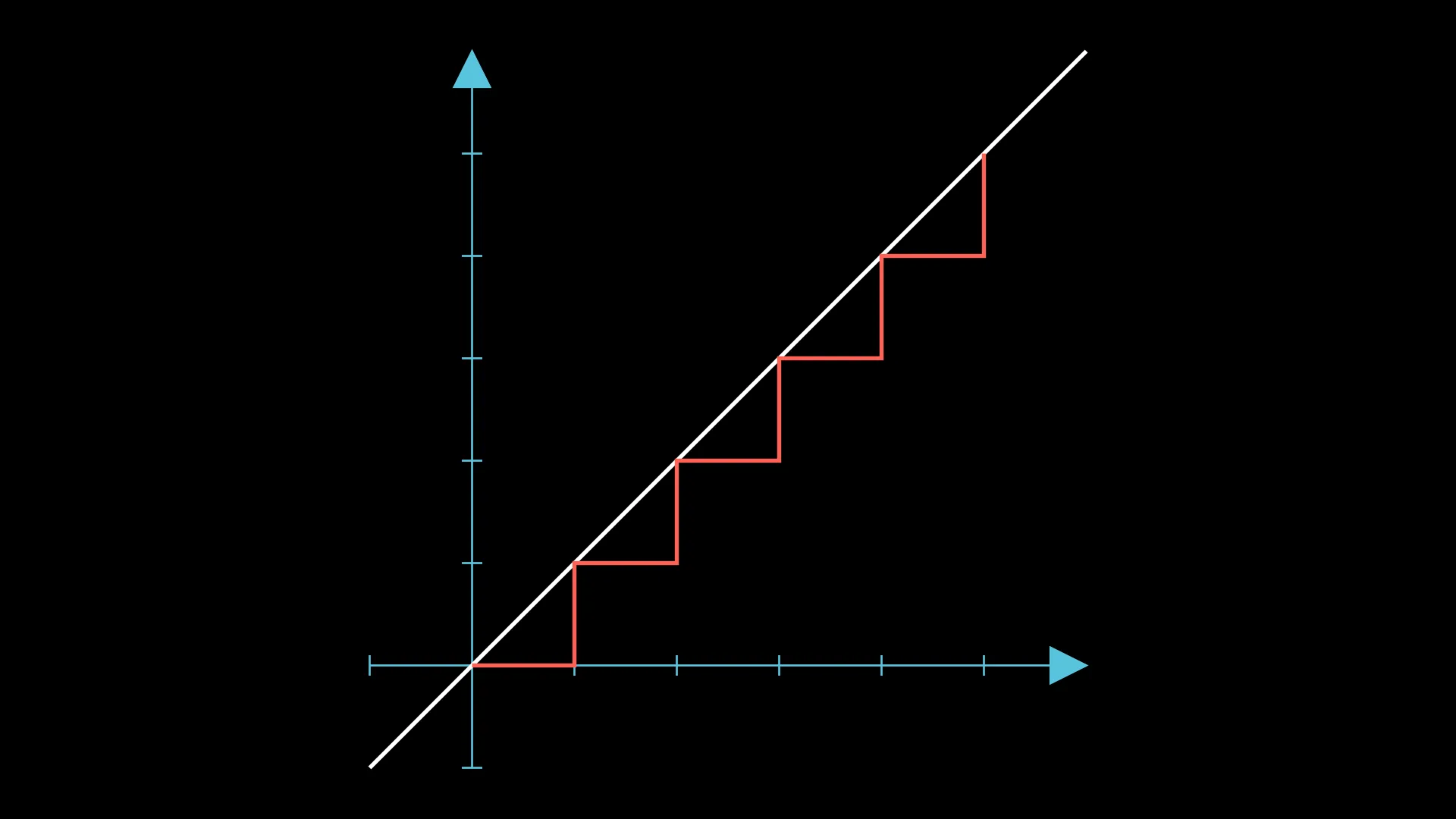
Currently, the configuration has 5 groups; how can we get it down to 4?

An obvious move is to swap the first “BA” to “AB”, which will give us this:

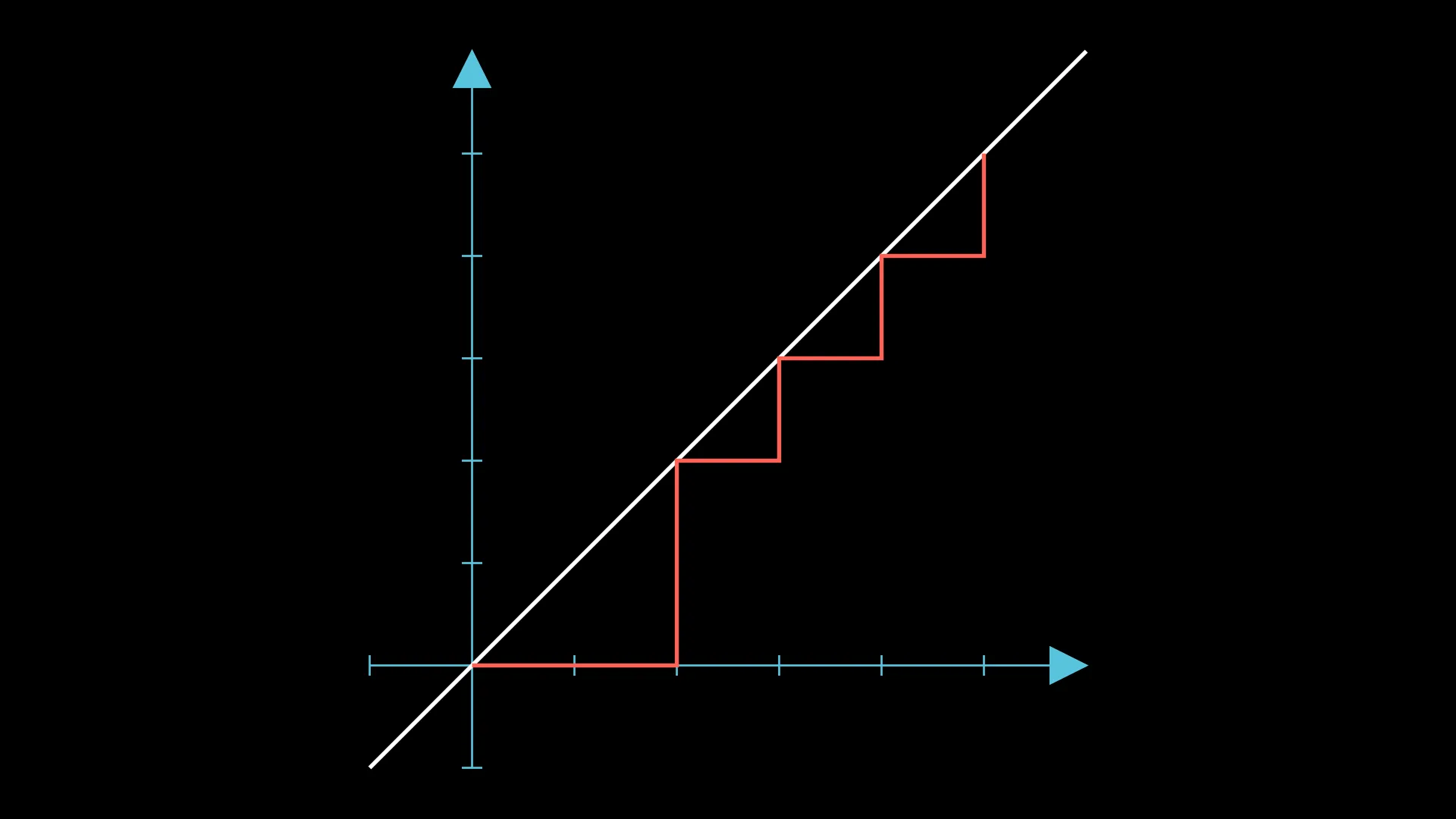
The visual interpretation for this is decreasing the height of a segment. Formally, if we decrease the height of 1 segment by $k$, it will require exactly $k$ swaps to do so (consider “AAAAAB”, for example).

Therefore, the problem has been reframed to the following—

Given a walk on a 2D plane, use increase/decrease height operations to:

1. ensure the walk remains below the line $y = x$
2. have the walk touch $y = x$ less than or equal to $k$ times

Brute Force

This problem reduces to an array partition problem, where the splits represent the points where the walk touches $y = x$. For instance, the walk above can be represented as the partition $\{[0, 2), [2, 3), [3, 4), [4, 5)\}$.

Let’s define $w(l, r)$ as the cost to form the partition $[l, r)$.

In the case above, $w(0, 2)$ would be 1, since one decrease height operation with $h = 1$ is required to form the desired right-triangle shape on that interval. $w(0, 5)$ would be 10, since we must decrease the height of all segments on $[1, 5)$, which have a total height of 10.

Thus, we can let $g(r, k)$ be the minimum cost to partition $[0, r)$ into $k$ segments, and write the following DP:

$$\begin{equation*} g(r, k) = \min_{0 \leq l < r} \{g(l, k-1) + w(l, r)\} \end{equation*}$$

This is easily doable in $\mathcal{O}(n^3)$ time.

Optimizing

Most of the optimization lies within the computation of $w(l, r)$, and finding an effective way to compute it basically gives you the rest of the problem. In conjunction with the fact that $g(r, k)$ is convex on $k$, we can achieve a $\mathcal{O}(n \log n)$ solution.

If you’re curious like I was about how to rigorously prove the convexity, it actually follows directly from the quadrangle inequality, which states that, for any such array partition problem, if the cost function $C(l, r)$ satisfies $C(a, c) + C(b, d) \leq C(a, d) + C(b, c)$ for all $a \leq b \leq c \leq d$, the cost of partitioning any interval $[l, r]$ is convex in the number of partitions.

A proof of this property is available here; you can find the proof by expanding the ‘定理3’ section and the one right below it. It’s written in Chinese, but you can probably ChatGPT the translation.

And that’s it for this problem! Here’s a link to my submission in case you get stuck.

My opinion on the problem: overall solid, but the statement is still a bit too contrived for my taste.