Welcome to my first ever problem editorial! Here’s a link to the problem (the page links an English PDF as well).

Observations

First, it is worth noting that any valid arrangement must be an RBS, where A’s are replaced with ’(’ and B’s with ’)’ (convince yourself that this is true).

Therefore, we consider visualizing our arrangement as a walk on a 2D plane, where A’s are right steps and B’s are up steps (note that if our arrangement is an RBS, this graph should never cross the line $y = x$). Here’s the visualization for the arrangement “AABBABAABB”:

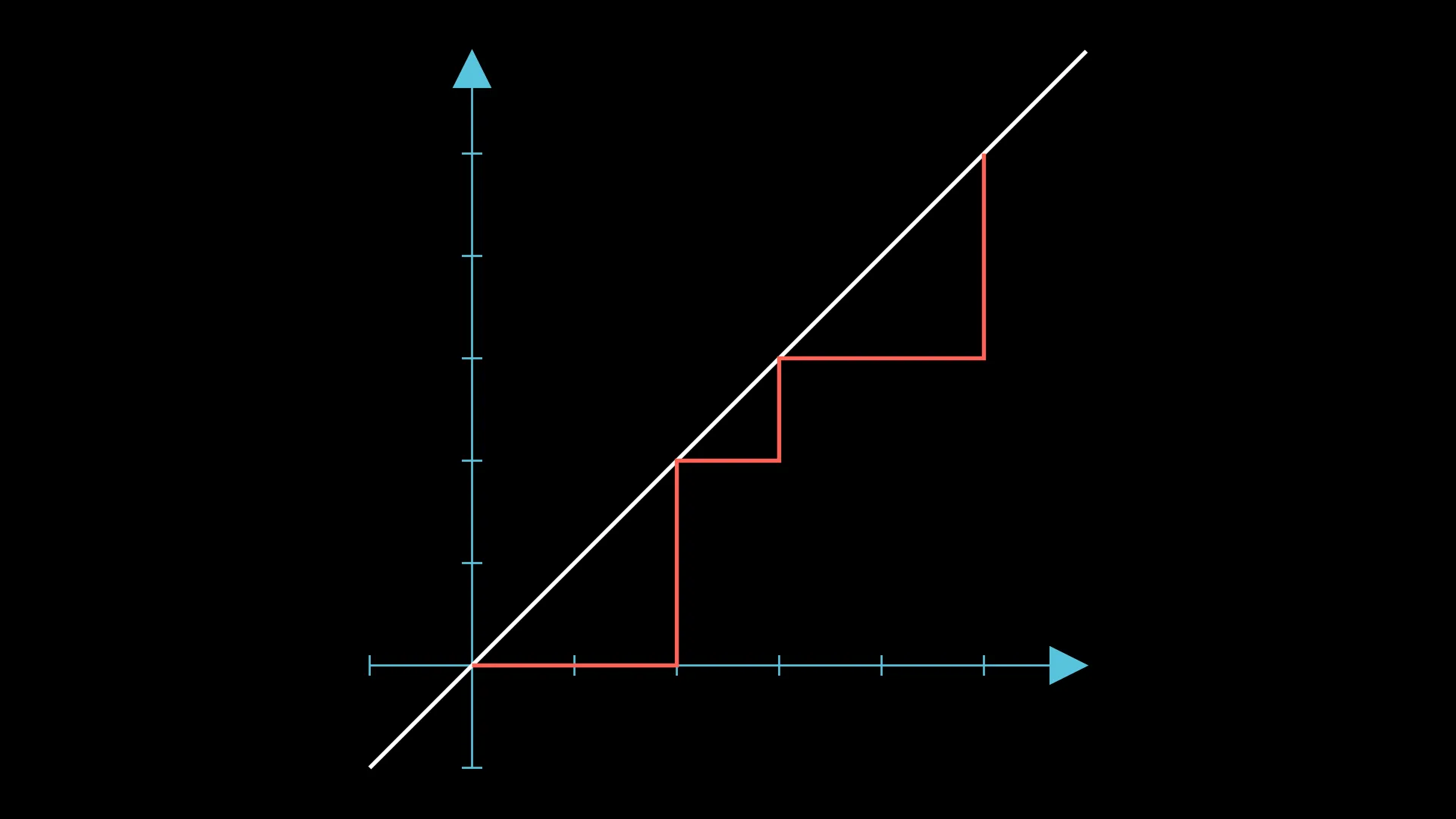
The maximum number of groups in this case is actually very obvious, since they are all contiguous—(AABB)(AB)(AABB). This can be seen visually as the number of times the walk touches the line $y = x$.

However, consider this case (which is one of the sample cases), “AABABABBAB”:

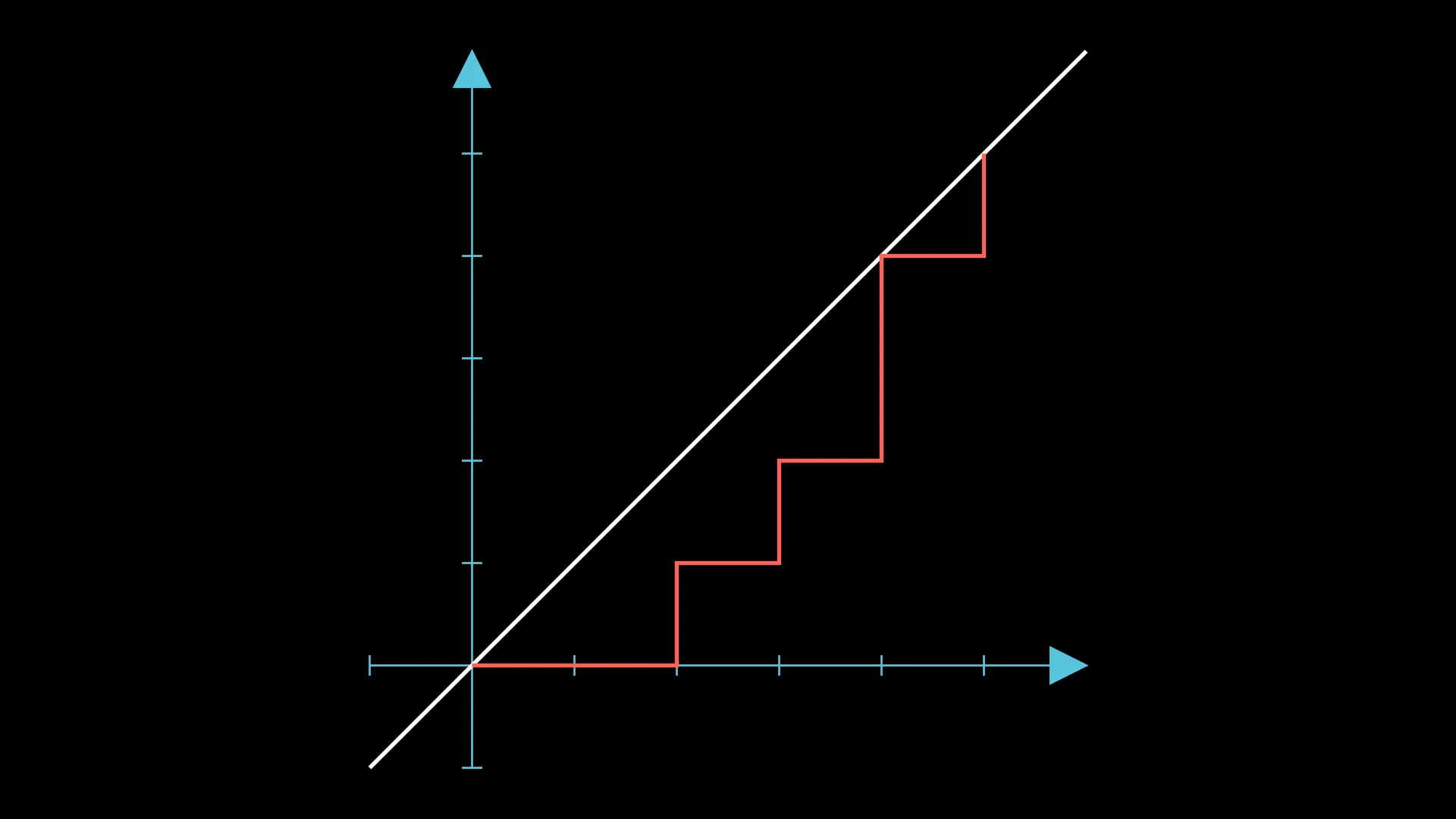
The maximum number of groups in this arrangement is also 3, but it is not as obvious as before. How can we transform this walk to make it easier to count the number of groups (i.e. such that the number of groups is exactly equal to the number of times the walk touches $y = x$)?

Here’s the same image, but with the groups colored this time:

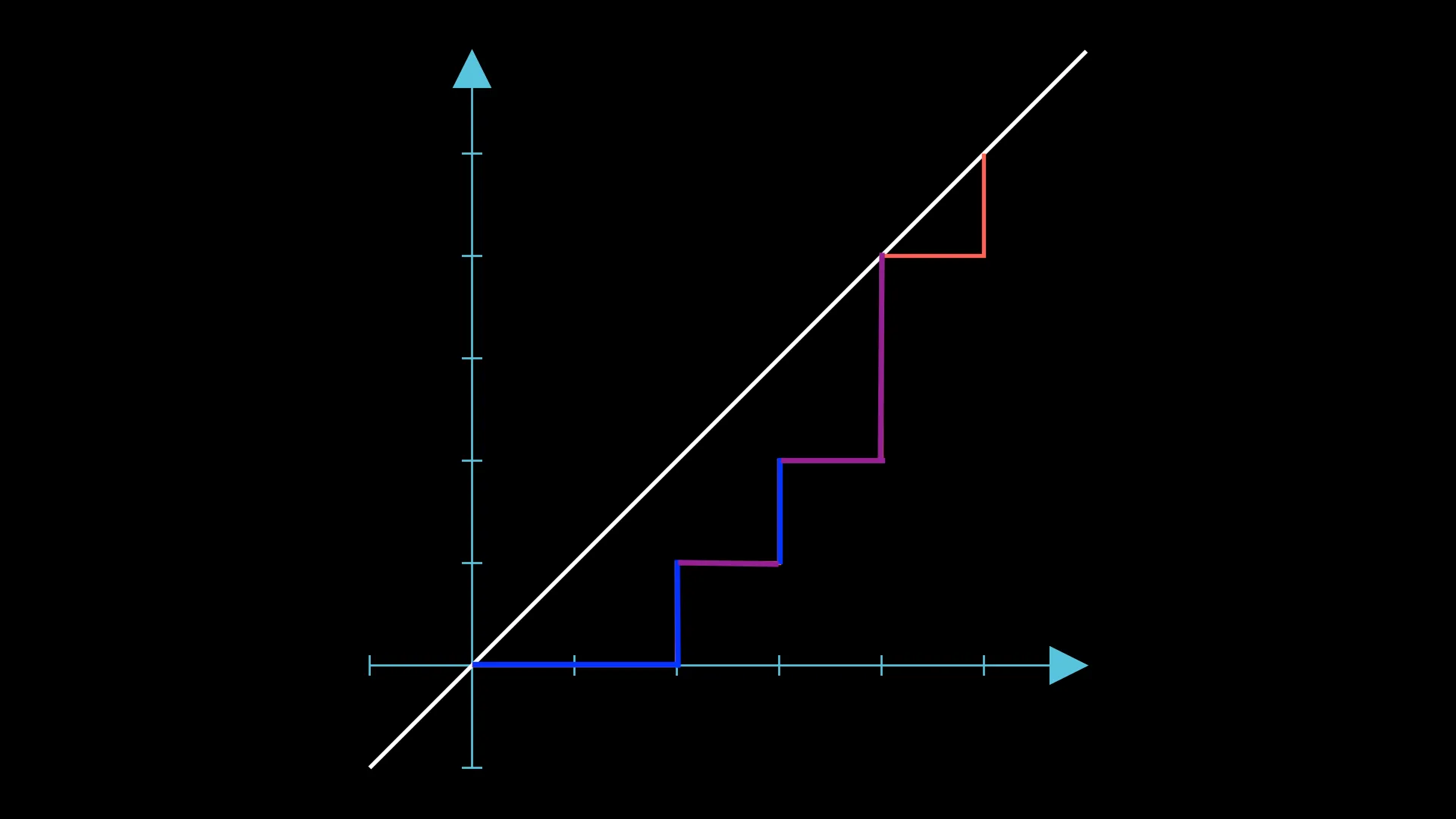
Notice how they are interleaved with each other; we would instead like every group to be disjoint. So, how can we achieve this?

Intuitively, we can “pull” the last blue segment forward and “push” the first purple segment up, which will give us this:

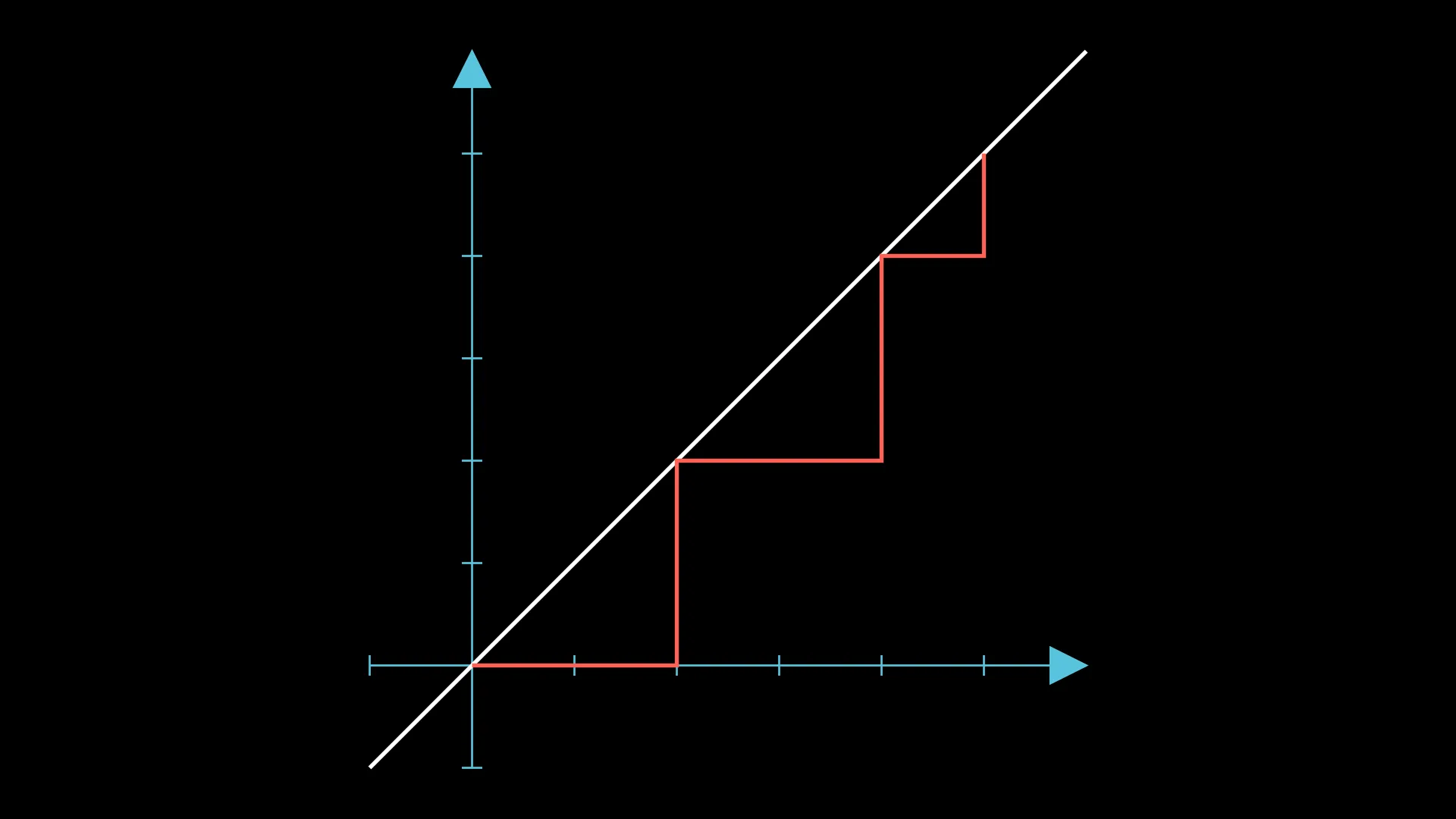
This can be seen even more intuitively as raising the height of a segment (in this case, the segment on $x = [2, 3)$).

Going back to the original problem, this operation is equivalent to swapping “AB” to “BA”, which can be shown to never actually decrease the answer (i.e. amount of groups formed).

So what operation will decrease the answer?

Consider the case where the initial arrangement is “ABABABABAB”. Here’s the walk for this arrangement:

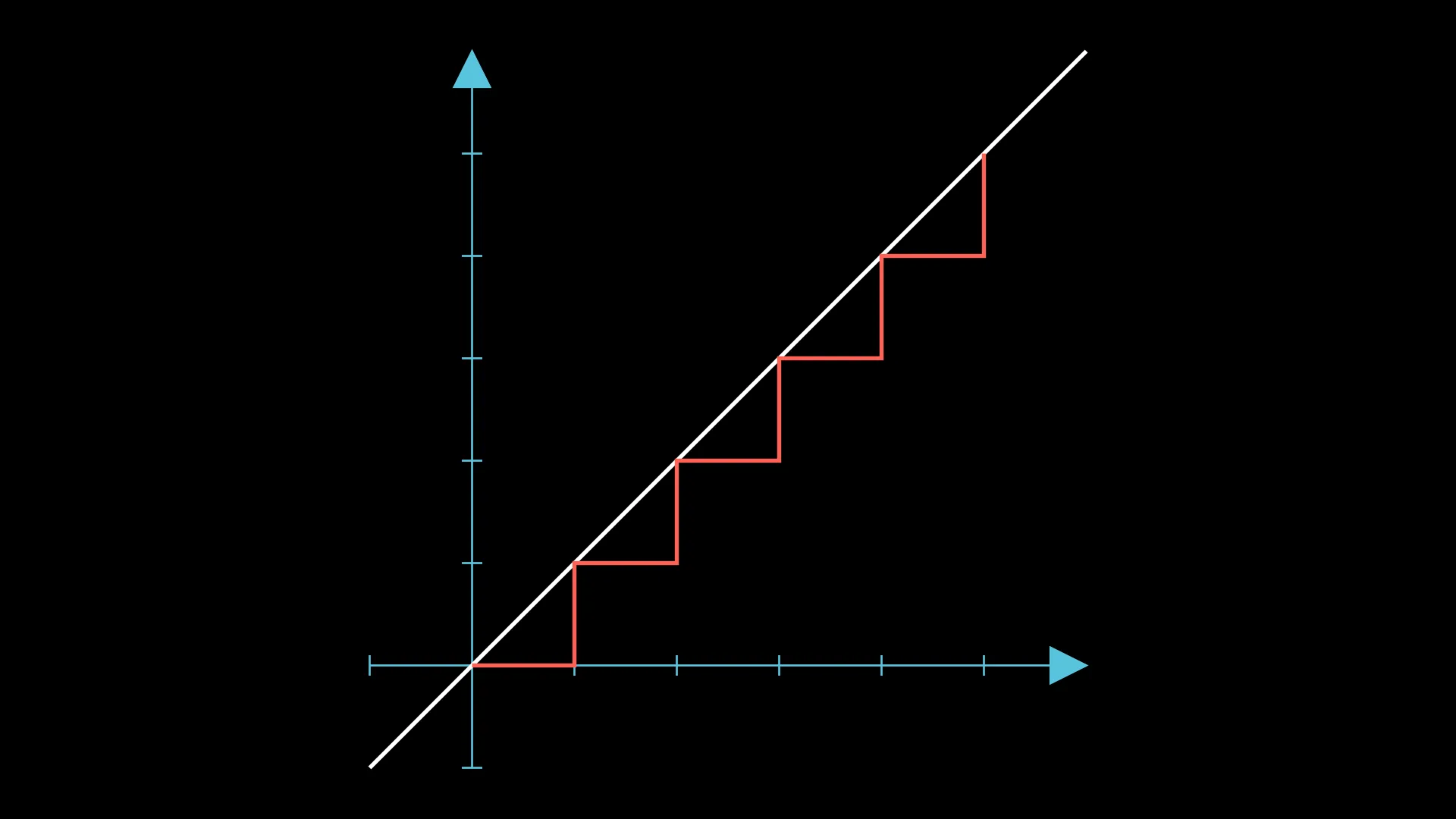
Currently, the configuration has 5 groups; how can we get it down to 4?

An obvious move is to swap the first “BA” to “AB”, which will give us this:

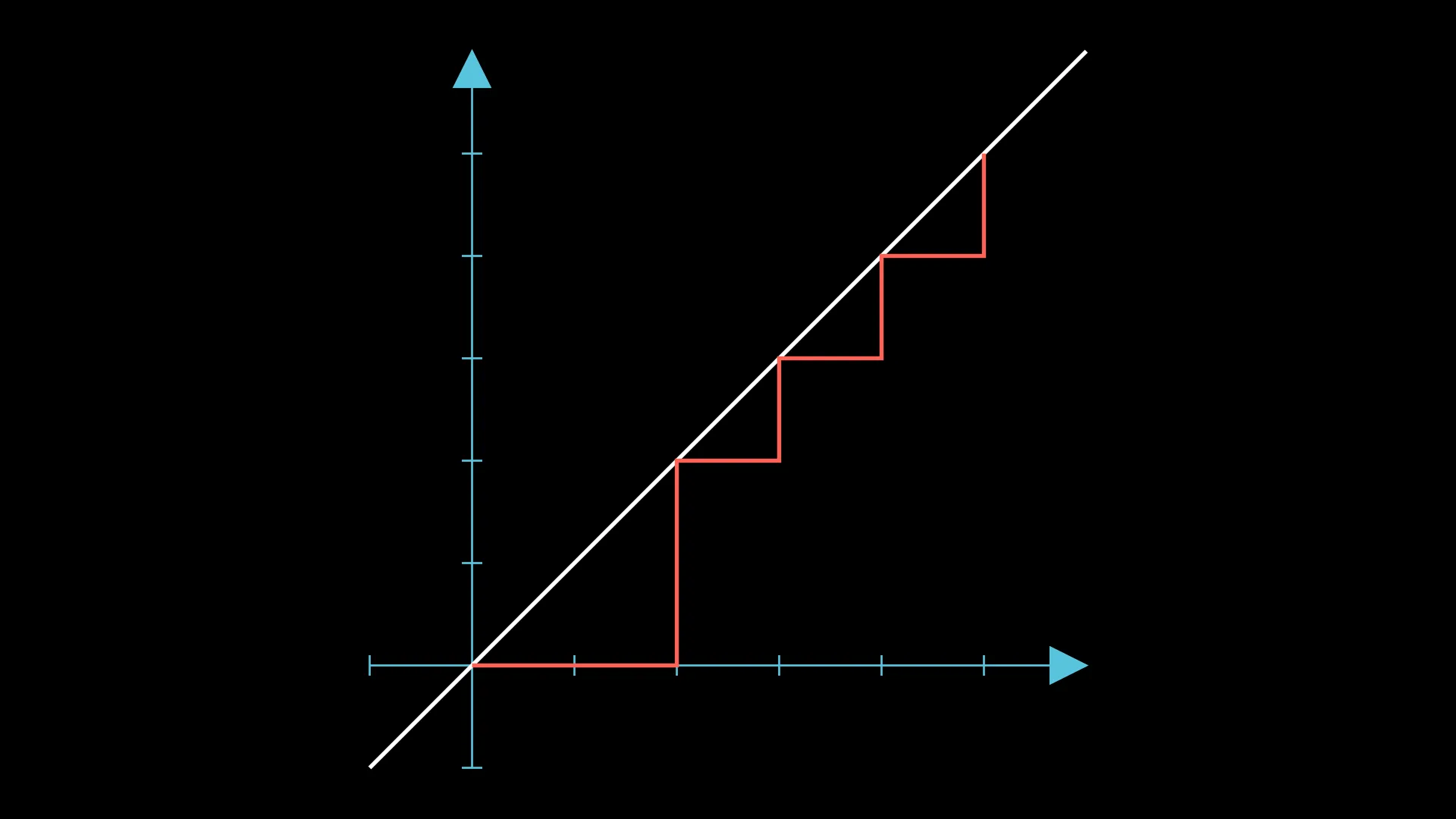
The visual interpretation for this is decreasing the height of a segment. Formally, if we decrease the height of 1 segment by $k$, it will require exactly $k$ swaps to do so (consider “AAAAAB”, for example).

Therefore, the problem has been reframed to the following—

Given a walk on a 2D plane, use increase/decrease height operations to:

1. ensure the walk remains below the line $y = x$
2. have the walk touch $y = x$ less than or equal to $k$ times

Brute Force

This problem reduces to an array partition problem, where the splits represent the points where the walk touches $y = x$. For instance, the walk above can be represented as the partition $\{[0, 2), [2, 3), [3, 4), [4, 5)\}$.

Let’s define $w(l, r)$ as the cost to form the partition $[l, r)$.

In the case above, $w(0, 2)$ would be 1, since one decrease height operation with $h = 1$ is required to form the desired right-triangle shape on that interval. $w(0, 5)$ would be 10, since we must decrease the height of all segments on $[1, 5)$, which have a total height of 10.

Thus, we can let $g(r, k)$ be the minimum cost to partition $[0, r)$ into $k$ segments, and write the following DP:

$$\begin{equation*} g(r, k) = \min_{0 \leq l < r} \{g(l, k-1) + w(l, r)\} \end{equation*}$$

This is easily doable in $\mathcal{O}(n^3)$ time.

Optimizing

Most of the optimization lies within the computation of $w(l, r)$, and finding an effective way to compute it basically gives you the rest of the problem. In conjunction with the fact that $g(r, k)$ is convex on $k$, we can achieve a $\mathcal{O}(n \log n)$ solution.

If you’re curious like I was about how to rigorously prove the convexity, it actually follows directly from the quadrangle inequality, which states that, for any such array partition problem, if the cost function $C(l, r)$ satisfies $C(a, c) + C(b, d) \leq C(a, d) + C(b, c)$ for all $a \leq b \leq c \leq d$, the cost of partitioning any interval $[l, r]$ is convex in the number of partitions.

A proof of this property is available here; you can find the proof by expanding the ‘定理3’ section and the one right below it. It’s written in Chinese, but you can probably ChatGPT the translation.

And that’s it for this problem! Here’s a link to my submission in case you get stuck.

My opinion on the problem: overall solid, but the statement is still a bit too contrived for my taste.

Recently, I stumbled across the idea of functional programming (FP) and its flagship language, Haskell. I was instantly intrigued by the language’s unique syntax and simplicity. For instance, below are two implementations of a leftist heap in Java and Haskell, respectively:

public Node merge(Node x, Node y) {
    if (x == null)
        return y;
    if (y == null)
        return x;

    // if this were a max-heap, then the
    // next line would be: if (x.element < y.element)
    if (x.element.compareTo(y.element) > 0)
        // x.element > y.element
        return merge (y, x);

    x.rightChild = merge(x.rightChild, y);

    if (x.leftChild == null) {
        // left child doesn't exist, so move right child to the left side
        x.leftChild = x.rightChild;
        x.rightChild = null;
        // x.s was, and remains, 1
    } else {
        // left child does exist, so compare s-values
        if (x.leftChild.s < x.rightChild.s) {
            Node temp = x.leftChild;
            x.leftChild = x.rightChild;
            x.rightChild = temp;
        }
        // since we know the right child has the lower s-value, we can just
        // add one to its s-value
        x.s = x.rightChild.s + 1;
    }
    return x;
}

Ugly, as expected of Java.

compared to…

data LHeap a
  = Leaf
  | Node a (LHeap a) (LHeap a)

rank :: LHeap a -> Integer
rank Leaf = 0
rank (Node _ _ r) = rank r + 1

merge :: Ord a => LHeap a -> LHeap a -> LHeap a
merge Leaf h = h
merge h Leaf = h
merge h@(Node a l r) h'@(Node a' _ _)
  | a > a'           = merge h' h
  | rank r' > rank l = Node a r' l
  | otherwise        = Node a l r'
  where r' = merge r h'

Clean, concise, and elegant.

With that said, here’s what I’ve learned so far about Haskell and functional programming!

What is Functional Programming?

Obviously, FP revolves around functions. An important property of functions in FP is that they are first-class citizens. This means that functions can be passed as arguments to other functions, returned as values from other functions, and assigned to variables. Functions also satisfy the referential transparency property, which means that a function always returns the same output for the same input.

Here’s a concrete example: imagine a Counter class in a standard OOP language with a method increment() that increments a counter by 1 and returns the new value. If you call increment() twice, the first call will return 1, while the second will return 2. However, in FP, you would define a function increment that takes a counter as an argument and returns a new counter with the value incremented by 1. Therefore, increment counter will always return the same value, regardless of how many times you call it.

let counter = 0
let counter1 = increment counter --will have value 1
let counter2 = increment counter --will have value 1
let counter3 = increment counter1 --will have value 2

A consequence of this is that all objects in FP are immutable, meaning that once an object is created, it cannot be modified. Instead, a new object is created with the desired changes. This means that code like this:

int a[10];
for (int i = 0; i < 5; i++) ++a[i];
// do stuff with a
for (int i = 5; i < 10; i++) ++a[i];
// do stuff with a

Has no simple FP equivalent. Instead, you would have to create a new array with the desired changes:

let a = replicate 10 0
let a' = incrementFirstFive a
-- do stuff with a'
let a'' = incrementLastFive a'
-- do stuff with a''

Which is obviously less efficient, as you have to copy the array twice. (Haskell does provide ways to get around this, which may be covered in a future post.)

A benefit of this immutability, however, is that all objects are fully persistent, meaning that all versions of an object are accessible at all times. For instance, in the C++ code above, only the final version of a is accessible at the end of the code. In Haskell, all versions of a (a, a', a'') are accessible at all times. This means that implementing a data structure efficiently in FP reaps the added benefit of having a fully persistent data structure. Functional data structures are an active area of research, and many data structures have already been developed that are both efficient and fully persistent. Some classic data structures that have purely functional equivalents are stacks, sets/multisets, and priority queues (you can read more about such data structures here).

Solving Some Problems

Let’s get our hands dirty by actually writing some code! I decided to turn to CSES, a collection of competitive programming problems, to practice my Haskell skills (or lack thereof).

Weird Algorithm

This problem just asks you to simulate the Collatz conjecture. Here’s the Haskell code:

collatz :: Int -> [Int] -- function signature: takes an Int and returns a list of Ints
-- Ex: collatz 3 = [3, 10, 5, 16, 8, 4, 2, 1]
collatz 1 = [1] -- base case: if n = 1, return [1]
-- (:) denotes prepending a single value; 1:[2, 3] = [1, 2, 3]
collatz n = n:collatz (if even n then n `div` 2 else 3 * n + 1)

main :: IO()
main = do
  n <- readLn :: IO Int -- equivalent to int n; cin >> n;
  -- (.) denotes function composition: f . g x = f(g(x))
  -- ($) is used to avoid parentheses: f (g x) = f $ g x
  -- map applies a function to each element of a list (ex: map f [1, 2, 3] = [f 1, f 2, f 3])
  -- unwords concatenates a list of strings with spaces in between
  putStrLn . unwords . map show $ collatz n

Gray Code

This problem requires a little more thought, but is still relatively easy. Here’s the solution: if we have the Gray Code for $n - 1$, simply append 0 to the front of each number, and append 1 to the front of each number in reverse order. This will give us the Gray Code for $n$.

code :: Int -> [String]
code 0 = [""] -- base case
code n =
  let a = code (n - 1) -- defining a variable!
  -- (<$>) is an infix version of fmap: f <$> x = fmap f x
  -- ('0':) is a function that takes a string and prepends '0' to it
  -- Note that it's a partial form of something like '0':"123", which would evaluate to "0123"
  -- Similarly, (2+) <$> [1, 2, 3] = [3, 4, 5]
  -- '++' simply concatenates two lists
  in (('0':) <$> a) ++ (('1':) <$> reverse a)

main :: IO()
main = do
  n <- readLn :: IO Int
  -- unlines separates an array w/ newlines instead of spaces
  putStrLn . unlines $ code n

If you’ve done any kind of web dev, you’ve probably heard terms like: SSG, SSR, CSR, hydration, etc; but most documentation doesn’t do a great job at explaining what these actually are. So in this post, I’ll try and explain them to the best of my understanding!

SSG (Static Site Generation)

This is the most classical form of site deployment; it essentially means all your site’s HTML is generated at build time, allowing for it to be sent directly to the client when they request it. In fact, this website itself uses SSG, allowing for much faster load times compared to…

SSR (Server-Side Rendering)

Rather than build all the site’s HTML at once, SSR websites build pages only when a user queries for them. Compared to SSG, where the same about.html file will be sent to all clients who navigate to the About page, SSR will rebuild about.html each time a user queries for it before sending it back. While this approach may seem strictly worse at first, its use lies in dynamic routes. Take GitHub, for example: each user has a unique page at https://github.com/username, but with hundreds of millions of accounts, GitHub can’t possibly constantly rebuild each of these pages! Not to mention, any edit made to biographies or usernames would require a rebuild as well. However, with SSR, if I navigate to a page like https://github.com/danielzsh, GitHub is not only able to reply with the most up-to-date information but also has the luxury of “lazily” building the page only when a client tries to visit it, rather than constantly rebuilding it manually.

CSR (Client-Side Rendering)

<html>
 <head>
   <title> CSR App </title>
 </head>
 
 <body>
     <main id="app"> </main>
     <script src="index.js"> </script>
 </body>
</html>

Wow. Amazing website.

In all seriousness, the above code is essentially what a CSR app looks like. Well…for a frame or two, at least. That index.js script actually contains all the logic for both the site UI and client interactions (button clicks, for example)! At its core, it’s probably something like:

document.getElementById("app").innerHTML = /* the site! */

However, as you may have guessed, pure CSR has a huge initial overhead; the client has to load index.js in its entirety before they can view, let alone interact with the site at all—and since that JavaScript file contains essentially the whole site and all its different pages, it’s more than a minor issue! This brings us to…

Client-Side Hydration

Hydration combines the initial load speed of SSG/SSR with the blazing fast interactions provided by CSR. Popularized by React, the process first sends a scaffold of the webpage to the client with all the DOM elements and styles, but without any JavaScript (which contributes the bulk of CSR overhead). However, no JavaScript means things like buttons and the cards on this site’s homepage won’t work; that’s where hydration comes in! Rather than send the JavaScript along with the site, we now fetch it only after the site’s initial load. We can also optimize this through processes such as code splitting, which allows us to fetch the JS incrementally, chunks at a time; this allows us to, for example, fetch code first for buttons that are immediately presented to the client before for other buttons, located further down the page.

Pretty cool, right? But don’t just take my word for it; you can see this hydration process for yourself!

1. Navigate to this site’s homepage and open up Chrome DevTools.
2. Open the Network Conditions panel and select “Fast 3G” in the Network Throttling dropdown.
3. Reload the homepage, and observe!
4. Make sure to turn throttling off once you’re done, or your experience on this site may become significantly slower :)

Note: Network throttling is essentially a way to simulate a slow connection, which makes behavior like hydration much obvious even though it always happens, regardless of connection speed.

Hopefully, you saw the first ~/about card just there on its own for a bit, before the second ~/blog card popped into the background. That’s hydration in action! Note that because the cards are regular <a> anchor tags, you can still click them before the page fully hydrates. However, both the swipe functionality and even the stacked card effect itself require JavaScript; hence, they don’t immediately load.

So…

In conclusion: SSG for smaller sites, SSR for larger sites or sites without dynamic routes, CSR basically never, and hydration is already shipped with most frameworks, such as Next.js and Gatsby. Whew!

References

1. Gatsby article with really helpful diagrams
2. Nice Medium article

---

Feel free to leave any suggestions for this post here by opening an Issue or Pull Request!

This site is built with Astro, a beautiful framework you should definitely try out; I also used a bit of React and swiper.js to make the cards on the homepage. Here’s the source code in case you’re interested!

Some Design Inspiration

• https://vercel.com (for links)
• https://antfu.me (just for being a really cool website)
• Next.js template (for the card component)
• GitHub Blog (for the blog layout)